A Closed Form Solution to Natural Image Matting – 笔记
2020-7-17
# 完整计算流程
对于灰度图,每个像素的值满足:
转换一下可以得到:
假设在一个小窗口内,和都是常数,则有 (其中代表窗口内的每一个像素位置,窗口大小一般为)。
所以有能量函数:
它可以写成矩阵的形式:
记,,则上式写成:
在固定的情况下,求,记,,,即求。
其中:
求的梯度,令其梯度为0得最优解:
所以最优解代入能量函数中得到:
记(代表单位矩阵),则:
将写成:
由展开可得的第项(文末推导)
最终需要求解使得的值最小:
满足条件的有很多,所以需要给它加上额外的约束:scribbles:
(其中为包含scribbles的图像数据,是一个的矩阵。 用于指示scribbles覆盖的像素的位置,是一个的对角矩阵, 主对角线上的个值,属于scribbles的位置为1,矩阵其余位置都为0。)
为用户输入的先验数据赋予一定的权重,最终求解的能量函数为:
求该能量函数的梯度:
令梯度为0,获得最优解
由此获得的解析形式:
通过读代码可以发现,程序中就是通过求解方程 获得 的解
# 推导的第项
要求的第项, 其中, 代表第个窗口,以下,均针对第个窗口。
已知:
故可写成:
求的逆:
记为, 记为, 所以,计算:
计算:
计算(为单位矩阵):
因此,的第项为:
由23式可得:
所以24式所得的第项即的第项}
对于,其中,现找出同时包含第个像素和第个像素的所有窗口,窗口序号为,取的第项的值,累加便得到的第项。
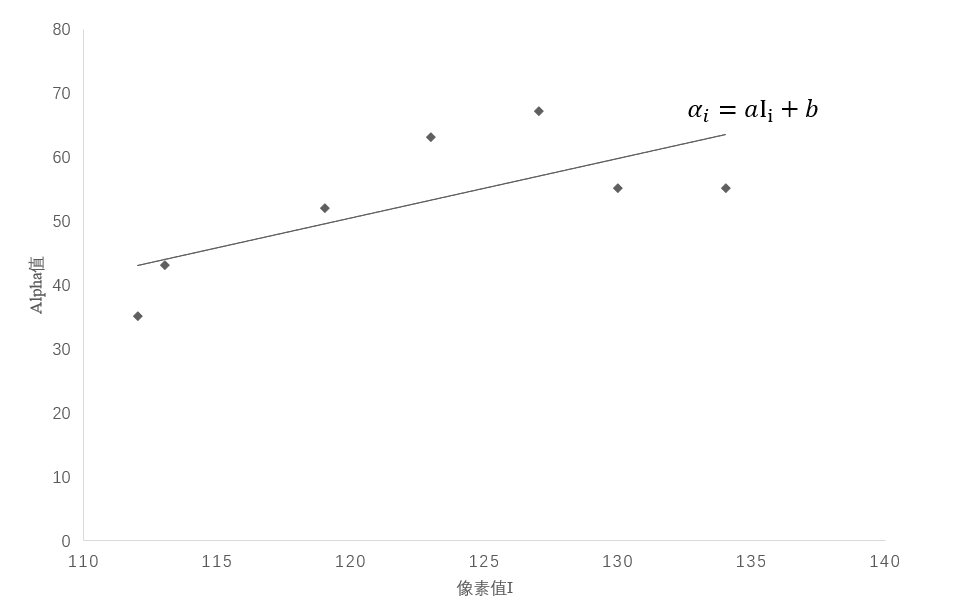
写的很完美,彩色照片的公式也解释下,就更秒了