DBSCAN – 基于密度的聚类算法

简单对比DBSCAN和K-Means

DBSCAN是基于密度的聚类算法，K-Means是基于划分的聚类算法

顾名思义，基于密度可以理解为将每一簇较为集中的数据聚为一类，基于划分可以理解为寻找一种划分方式尽可能地将每种类别划分开来

• 基于划分的K-Means算法需要一个参数 k，也就是需要指定聚多少类

• 基于密度的DBSCAN算法需要两个参数 max_r, min_pts，也就是需要指定寻找邻居的圈子大小（搜索半径）和指定发现多少个邻居算是足够密集（密度阈值）

封装好的DBSCAN算法

DBSCAN作为一项提出许久，而且十分成熟的聚类算法，和K-Means一样，都可以在scikit-learn这个机器学习库中找到封装好的实现代码

https://scikit-learn.org/stable/modules/generated/sklearn.cluster.DBSCAN.html#sklearn.cluster.DBSCAN。

动手实现DBSCAN算法

1# -*- "coding: utf-8" -*-
2# learning DBSCAN algorithm
3# author: hxhen
4
5''' About DBSCAN
6DBSCAN ( Density-Based Spatial Clustering of Applications with Noise, https://www.aaai.org/Papers/KDD/1996/KDD96-037.pdf)
7'''

准备数据集

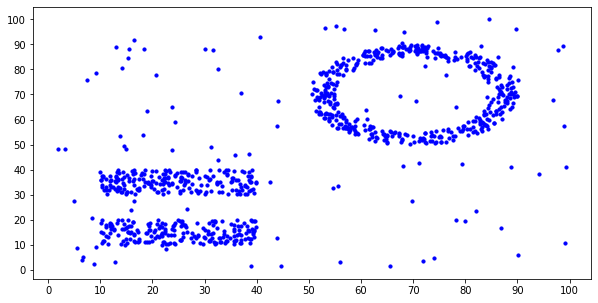
DBSCAN的优势就是在于能忽略噪声的影响，同时可以正确处理形状不规则的聚类问题，所以需要准备一个包含不规则簇的同时存在背景噪声的数据集。

我大致分为三步：

• 在100×100的范围内随机放置一些点，作为背景噪声
• 在左下角放两个平行矩形
• 在右上角放一个圆环
• （将这些坐标点的存放顺序打乱）

下面是数据准备的代码和准备好的数据的效果：

1import numpy as np
2import matplotlib.pyplot as plt
3import copy

 1# initialize dataset
 2dataset = [(100*np.random.random(), 100*np.random.random()) for i in range(100)]  # random point as background
 3dataset += [(30*np.random.random()+10, 10*np.random.random()+10) for i in range(200)]  # add a rectangular size (30, 10)
 4dataset += [(30*np.random.random()+10, 10*np.random.random()+30) for i in range(200)]  # add another rectangular size (30, 10)
 5for i in range(2000):  # add a oval ring at up right corner
 6    x = 50*np.random.random()+50
 7    y = 50*np.random.random()+50
 8    if 15 < np.sqrt((x-70)**2 + (y-70)**2) < 20:
 9        dataset.append((x, y))
10
11np.random.shuffle(dataset)  # shuffle the points
12
13plt.figure(figsize=(10,5))  # (width, height)
14plt.scatter([item[0] for item in dataset], [item[1] for item in dataset], c='b', s=10)
15plt.xticks(np.arange(0, 101, 10))
16plt.yticks(np.arange(0, 101, 10))
17plt.show()

使用DBSCAN进行聚类

算法大致分为这么几步：

• 随机从一个坐标点开始，寻找半径max_r范围内的所有邻居坐标点。

• 如果邻居的数量小于min_pts，则判定为孤立点，不分配到任何一个簇中

• 如果邻居的数量大于min_pts，则创建一个新簇，将当前坐标点作为簇的第一个成员，然后检查它的所有邻居，如果有哪个邻居还没有被分配到任何一个簇当中，就将它归为当前簇。同时，如果某个邻居它自己的邻居数量也超过了min_pts，也要按同样的方式检查它的邻居。

• 直到数据集的所有坐标点都被检查一遍，算法结束

下面是实现的代码以及聚类后的效果图：

 1#-------- DBSCAN --------#
 2
 3max_r = 5  # radius threshold
 4min_pts = 10  # neighbors threshold
 5clusters = []  # store clusters
 6
 7def find_neighbors(point):
 8    p_x, p_y = point
 9    neighbors = []
10    for x, y in dataset:
11        distance = np.sqrt((p_x-x)**2 + (p_y-y)**2)
12        if distance < max_r:
13            neighbors.append((x, y))
14    return neighbors
15
16def find_cluster(point):
17    for idx, cluster in enumerate(clusters):
18        if point in cluster:
19            return idx
20    return -1
21
22points = copy.deepcopy(dataset)
23for point in dataset:
24    if point not in points:  # this point belongs to one cluster already, skip it.
25        continue
26    points.remove(point)
27    neighbors = find_neighbors(point)
28    pts = len(neighbors)
29    if pts > min_pts:  # create a new cluster and check this point's neighbors
30        cluster = [point]
31        for neigh in neighbors:
32            if neigh in points:
33                points.remove(neigh)
34                if find_cluster(neigh) == -1:  # this neighbor has not been clustered
35                    cluster.append(neigh)
36                neigh_neighbors = find_neighbors(neigh)
37                if len(neigh_neighbors) > min_pts:
38                    neighbors += neigh_neighbors
39        clusters.append(cluster)
40
41print("find {} clusters".format(len(clusters)))
42# visualize the result
43colors = ['red', 'orange', 'yellow', 'green', 'purple', 'black']
44plt.figure(figsize=(10,5))  # (width, height)
45plt.xticks(np.arange(0, 101, 10))
46plt.yticks(np.arange(0, 101, 10))
47for point in dataset:
48    idx = find_cluster(point)
49    if idx == -1:
50        plt.scatter(point[0], point[1], c='b', s=10)
51    else:
52        plt.scatter(point[0], point[1], c=colors[idx], s=10)
53plt.show()

1find 3 clusters

拿K-Means算法作对比

为了更好地体现两个聚类算法的区别，我在以前实现的聚两类的K-Means算法基础上修改得到完整的K-Means算法，用这个算法指定聚3类，对同一个数据集进行聚类，然后观察K-Means在这个数据集上的聚类效果。

 1#-------- K-Means --------#
 2
 3import random
 4
 5X = dataset
 6max_iteration = 300  # 最大迭代次数
 7k = 3  # 聚k类
 8clusters = []  # 保存聚类结果
 9centers = [random.choice(X) for x in range(k)]  # 初始化质心，此处在数据集中随机选两个质心
10
11for iteration in range(max_iteration):
12    clusters = []
13    for x in X:
14        distances = [(x[0]-center[0])**2+(x[1]-center[1])**2 for center in centers]  # 计算点到各质心的距离
15        clusters.append(np.argmin(distances))  # 根据距离归类，类别为距离最近的一类
16    # 根据归类结果划分数据
17    predicts = [[] for i in range(k)]
18    for index, x in enumerate(X):
19        predicts[clusters[index]].append(x)
20    # 重新计算质心
21    temp_centers = []
22    for predict in predicts:
23        temp_center = (sum([x[0] for x in predict])/len(predict), sum([x[1] for x in predict])/len(predict))
24        temp_centers.append(temp_center)
25    if temp_centers == centers:  # 质心不再变化
26        print("End at iteration:", iteration)
27        break
28    else:
29        centers = copy.deepcopy(temp_centers)
30
31# 可视化聚类结果
32plt.figure(figsize=(10,5))  # (width, height)
33plt.xticks(np.arange(0, 101, 10))
34plt.yticks(np.arange(0, 101, 10))
35colors = ['red', 'orange', 'yellow', 'green', 'purple', 'black']
36plt.scatter([x[0] for x in X], [x[1] for x in X], c=[colors[x] for x in clusters], s=10)
37plt.scatter([x[0] for x in centers], [x[1] for x in centers], c=colors[:k], marker="X", s=100)

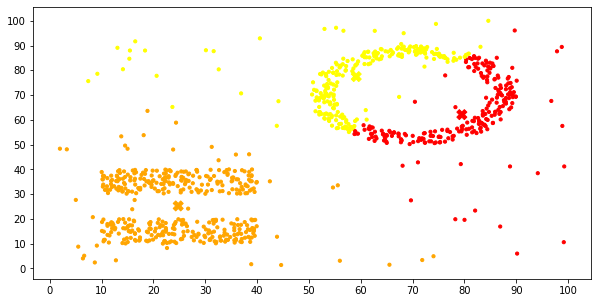
可以很明显地发现，基础的K-Means算法没有对噪音数据做特殊处理，所以在噪音数据的影响下，划分显得很勉强，而且，对于圆环，矩形这种簇的形状识别的也不好。

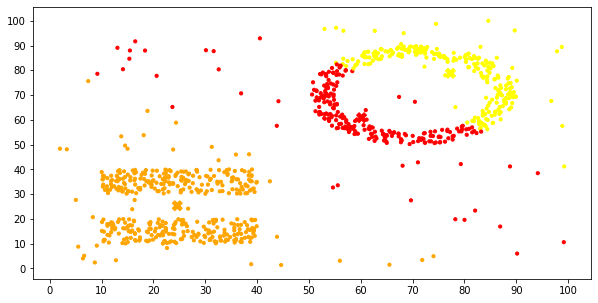
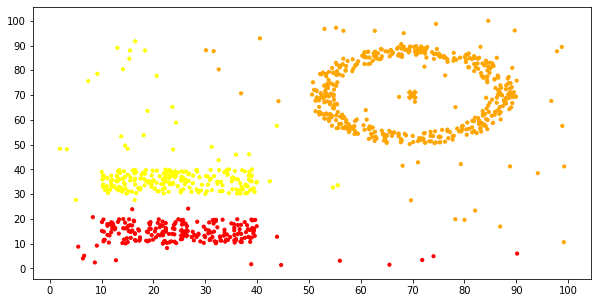
多执行几次，可以看到不同的聚类效果，偶尔也能得到近乎正确的结果：

参考资料

• 《商务智能方法与应用》（刘红岩编著）

更多阅读

• DBSCAN 算法的论文 Density-Based Spatial Clustering of Applications with Noise

  https://www.aaai.org/Papers/KDD/1996/KDD96-037.pdf

• 我以前写的K-Means算法简单实现

  http://60.205.204.113/k-means-cluster-implements/

  哈哈~

(在线排版工具使用的是http://md.aclickall.com/)，感谢！